Note
Go to the end to download the full example code. or to run this example in your browser via Binder
Source detection and significance maps#
Build a list of significant excesses in a Fermi-LAT map.
Context#
The first task in a source catalog production is to identify significant excesses in the data that can be associated to unknown sources and provide a preliminary parametrization in terms of position, extent, and flux. In this notebook we will use Fermi-LAT data to illustrate how to detect candidate sources in counts images with known background.
Objective: build a list of significant excesses in a Fermi-LAT map
Proposed approach#
This notebook show how to do source detection with Gammapy using the
methods available in estimators. We will use images from a
Fermi-LAT 3FHL high-energy Galactic center dataset to do this:
perform adaptive smoothing on counts image
produce 2-dimensional test-statistics (TS)
run a peak finder to detect point-source candidates
compute Li & Ma significance images
estimate source candidates radius and excess counts
Note that what we do here is a quick-look analysis, the production of real source catalogs use more elaborate procedures.
We will work with the following functions and classes:
Setup#
As always, let’s get started with some setup …
import numpy as np
import astropy.units as u
# %matplotlib inline
import matplotlib.pyplot as plt
from IPython.display import display
from gammapy.datasets import MapDataset
from gammapy.estimators import ASmoothMapEstimator, TSMapEstimator
from gammapy.estimators.utils import find_peaks, find_peaks_in_flux_map
from gammapy.irf import EDispKernelMap, PSFMap
from gammapy.maps import Map
from gammapy.modeling.models import PointSpatialModel, PowerLawSpectralModel, SkyModel
Check setup#
from gammapy.utils.check import check_tutorials_setup
check_tutorials_setup()
System:
python_executable : /Users/mregeard/Workspace/dev/code/gammapy/gammapy/.tox/build_docs/bin/python
python_version : 3.11.10
machine : x86_64
system : Darwin
Gammapy package:
version : 1.3.dev1205+g00f44f94ac
path : /Users/mregeard/Workspace/dev/code/gammapy/gammapy/.tox/build_docs/lib/python3.11/site-packages/gammapy
Other packages:
numpy : 1.26.4
scipy : 1.14.1
astropy : 5.2.2
regions : 0.10
click : 8.1.7
yaml : 6.0.2
IPython : 8.28.0
jupyterlab : not installed
matplotlib : 3.9.2
pandas : not installed
healpy : 1.17.3
iminuit : 2.30.1
sherpa : 4.16.1
naima : 0.10.0
emcee : 3.1.6
corner : 2.2.2
ray : 2.37.0
Gammapy environment variables:
GAMMAPY_DATA : /Users/mregeard/Workspace/dev/code/gammapy/gammapy-data/
Read in input images#
We first read the relevant maps:
counts = Map.read("$GAMMAPY_DATA/fermi-3fhl-gc/fermi-3fhl-gc-counts-cube.fits.gz")
background = Map.read(
"$GAMMAPY_DATA/fermi-3fhl-gc/fermi-3fhl-gc-background-cube.fits.gz"
)
exposure = Map.read("$GAMMAPY_DATA/fermi-3fhl-gc/fermi-3fhl-gc-exposure-cube.fits.gz")
psfmap = PSFMap.read(
"$GAMMAPY_DATA/fermi-3fhl-gc/fermi-3fhl-gc-psf-cube.fits.gz",
format="gtpsf",
)
edisp = EDispKernelMap.from_diagonal_response(
energy_axis=counts.geom.axes["energy"],
energy_axis_true=exposure.geom.axes["energy_true"],
)
dataset = MapDataset(
counts=counts,
background=background,
exposure=exposure,
psf=psfmap,
name="fermi-3fhl-gc",
edisp=edisp,
)
/Users/mregeard/Workspace/dev/code/gammapy/gammapy/.tox/build_docs/lib/python3.11/site-packages/astropy/wcs/wcs.py:803: FITSFixedWarning: 'datfix' made the change 'Set DATEREF to '2001-01-01T00:01:04.184' from MJDREF.
Set MJD-OBS to 54682.655283 from DATE-OBS.
Set MJD-END to 57236.967546 from DATE-END'.
warnings.warn(
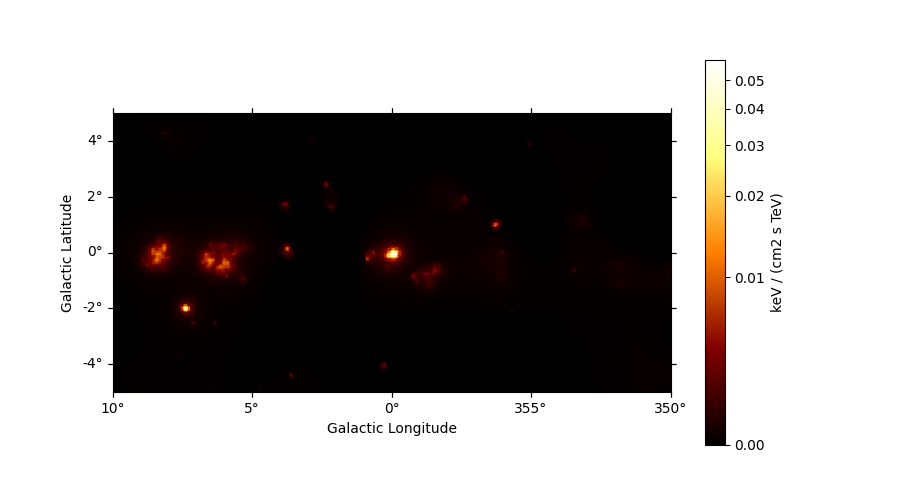
Adaptive smoothing#
For visualisation purpose it can be nice to look at a smoothed counts image. This can be performed using the adaptive smoothing algorithm from Ebeling et al. (2006).
In the following example the ASmoothMapEstimator.threshold argument gives the minimum
significance expected, values below are clipped.
scales = u.Quantity(np.arange(0.05, 1, 0.05), unit="deg")
smooth = ASmoothMapEstimator(threshold=3, scales=scales, energy_edges=[10, 500] * u.GeV)
images = smooth.run(dataset)
plt.figure(figsize=(9, 5))
images["flux"].plot(add_cbar=True, stretch="asinh")
plt.show()
TS map estimation#
The Test Statistic, \(TS = 2 \Delta log L\) (Mattox et al. 1996), compares the likelihood function L optimized with and without a given source. The TS map is computed by fitting by a single amplitude parameter on each pixel as described in Appendix A of Stewart (2009). The fit is simplified by finding roots of the derivative of the fit statistics (default settings use Brent’s method).
We first need to define the model that will be used to test for the existence of a source. Here, we use a point source.
spatial_model = PointSpatialModel()
# We choose units consistent with the map units here...
spectral_model = PowerLawSpectralModel(amplitude="1e-22 cm-2 s-1 keV-1", index=2)
model = SkyModel(spatial_model=spatial_model, spectral_model=spectral_model)
Here we show a full configuration of the estimator. We remind the user of the meaning of the various quantities:
model: aSkyModelwhich is converted to a source model kernelkernel_width: the width for the above kerneln_sigma: number of sigma for the flux errorn_sigma_ul: the number of sigma for the flux upper limitsselection_optional: what optional maps to computen_jobs: for running in parallel, the number of processes used for the computationsum_over_energy_groups: to sum over the energy groups or fit thenormon the full energy cube
estimator = TSMapEstimator(
model=model,
kernel_width="1 deg",
energy_edges=[10, 500] * u.GeV,
n_sigma=1,
n_sigma_ul=2,
selection_optional=None,
n_jobs=1,
sum_over_energy_groups=True,
)
maps = estimator.run(dataset)
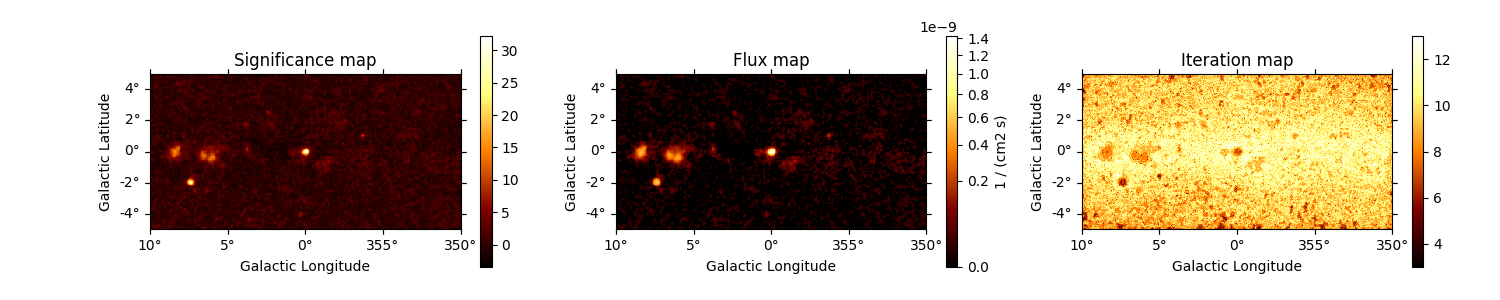
Accessing and visualising results#
Below we print the result of the TSMapEstimator. We have access to a number of
different quantities, as shown below. We can also access the quantities names
through map_result.available_quantities.
print(maps)
FluxMaps
--------
geom : WcsGeom
axes : ['lon', 'lat', 'energy']
shape : (400, 200, 1)
quantities : ['ts', 'norm', 'niter', 'norm_err', 'npred', 'npred_excess', 'stat', 'stat_null', 'success']
ref. model : pl
n_sigma : 1
n_sigma_ul : 2
sqrt_ts_threshold_ul : 2
sed type init : likelihood
fig, (ax1, ax2, ax3) = plt.subplots(
ncols=3,
figsize=(20, 3),
subplot_kw={"projection": counts.geom.wcs},
gridspec_kw={"left": 0.1, "right": 0.98},
)
maps["sqrt_ts"].plot(ax=ax1, add_cbar=True)
ax1.set_title("Significance map")
maps["flux"].plot(ax=ax2, add_cbar=True, stretch="sqrt", vmin=0)
ax2.set_title("Flux map")
maps["niter"].plot(ax=ax3, add_cbar=True)
ax3.set_title("Iteration map")
plt.show()
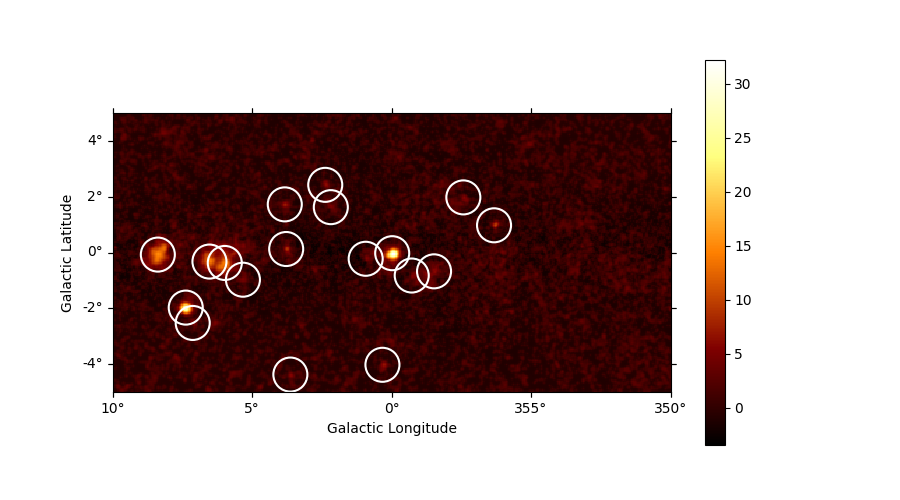
The flux in each pixel is obtained by multiplying a reference model with a normalisation factor:
print(maps.reference_model)
SkyModel
Name : 0aBSteC3
Datasets names : None
Spectral model type : PowerLawSpectralModel
Spatial model type : PointSpatialModel
Temporal model type :
Parameters:
index : 2.000 +/- 0.00
amplitude : 1.00e-22 +/- 0.0e+00 1 / (cm2 keV s)
reference (frozen): 1.000 TeV
lon_0 : 0.000 +/- 0.00 deg
lat_0 : 0.000 +/- 0.00 deg
maps.norm.plot(add_cbar=True, stretch="sqrt")
plt.show()
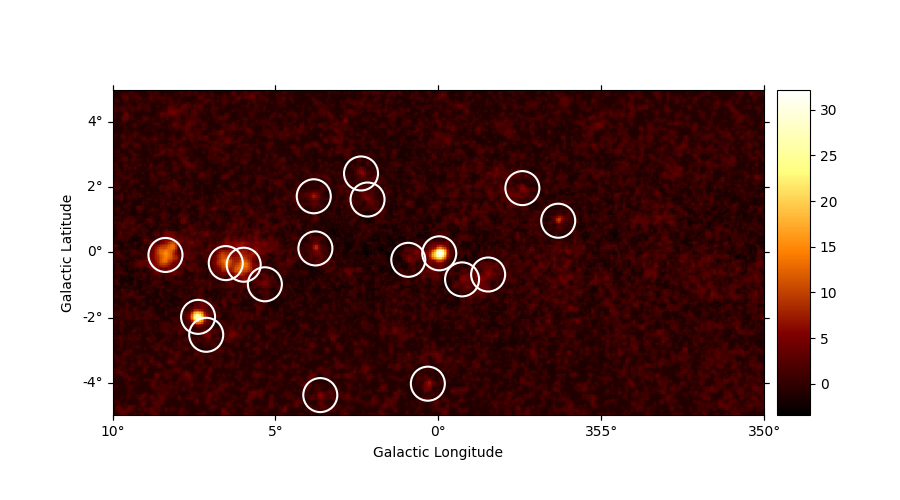
Source candidates#
Let’s run a peak finder on the sqrt_ts image to get a list of
point-sources candidates (positions and peak sqrt_ts values). The
find_peaks function performs a local maximum search in a sliding
window, the argument min_distance is the minimum pixel distance
between peaks (smallest possible value and default is 1 pixel).
sources = find_peaks(maps["sqrt_ts"], threshold=5, min_distance="0.25 deg")
nsou = len(sources)
display(sources)
# Plot sources on top of significance sky image
plt.figure(figsize=(9, 5))
ax = maps["sqrt_ts"].plot(add_cbar=True)
ax.scatter(
sources["ra"],
sources["dec"],
transform=ax.get_transform("icrs"),
color="none",
edgecolor="w",
marker="o",
s=600,
lw=1.5,
)
plt.show()
# sphinx_gallery_thumbnail_number = 3
value x y ra dec
deg deg
------ --- --- --------- ---------
32.194 200 99 266.41449 -28.97054
27.833 52 60 272.43197 -23.54282
15.16 32 98 271.16056 -21.74479
14.134 69 93 270.40919 -23.47797
13.872 80 92 270.15899 -23.98049
9.7638 273 119 263.18257 -31.52587
8.793 124 102 268.46711 -25.63326
7.3491 123 134 266.97596 -24.77174
6.8071 193 19 270.59696 -30.69138
6.2432 152 148 265.48068 -25.64323
5.8704 230 86 266.15140 -30.58926
5.6678 127 12 272.77351 -27.97934
5.6557 251 139 262.90685 -30.05853
5.4712 181 95 267.17020 -28.26173
5.4209 214 83 266.78188 -29.98429
5.1736 57 49 272.82739 -24.02653
5.067 156 132 266.12148 -26.23306
5.0414 93 80 270.37773 -24.84233
We can also utilise find_peaks_in_flux_map
to display various parameters from the FluxMaps
sources_flux_map = find_peaks_in_flux_map(maps, threshold=5, min_distance="0.25 deg")
display(sources_flux_map)
x y ra dec ts norm niter norm_err npred npred_excess stat stat_null success flux flux_err
deg deg 1 / (cm2 s) 1 / (cm2 s)
--- --- --------- --------- ---------- --------- ----- -------- ---------- ------------ ---------- ---------- ------- ----------- -----------
93 80 270.37773 -24.84233 25.41555 8.27043 8.0 2.37914 290.78937 27.07074 815.20556 840.62111 True 8.105e-11 2.332e-11
156 132 266.12148 -26.23306 25.67442 6.00005 8.0 1.89724 155.88363 19.73494 666.92009 692.59451 True 5.880e-11 1.859e-11
57 49 272.82739 -24.02653 26.76643 5.68610 7.0 1.76385 106.04843 18.55966 696.93904 723.70546 True 5.572e-11 1.729e-11
214 83 266.78188 -29.98429 29.38654 9.89249 9.0 2.63543 450.31686 32.72392 809.50127 838.88781 True 9.695e-11 2.583e-11
181 95 267.17020 -28.26173 29.93437 13.12076 9.0 3.22925 697.64626 43.25799 629.45787 659.39224 True 1.286e-10 3.165e-11
251 139 262.90685 -30.05853 31.98741 6.79990 8.0 1.95252 174.09938 22.54051 734.23408 766.22149 True 6.664e-11 1.913e-11
127 12 272.77351 -27.97934 32.12432 4.19126 8.0 1.37638 62.78010 13.76505 401.25085 433.37517 True 4.107e-11 1.349e-11
230 86 266.15140 -30.58926 34.46172 13.03987 9.0 3.10155 500.87813 43.20346 831.08719 865.54892 True 1.278e-10 3.040e-11
152 148 265.48068 -25.64323 38.97700 7.22434 8.0 1.91470 140.64858 23.74536 572.78773 611.76473 True 7.080e-11 1.876e-11
193 19 270.59696 -30.69138 46.33614 6.74666 8.0 1.74591 90.43161 22.28446 398.95343 445.28958 True 6.612e-11 1.711e-11
123 134 266.97596 -24.77174 54.00972 9.39519 7.0 2.16644 159.65186 30.82310 601.76247 655.77218 True 9.207e-11 2.123e-11
124 102 268.46711 -25.63326 77.31675 17.36545 9.0 3.11225 434.86369 56.97380 804.66583 881.98258 True 1.702e-10 3.050e-11
273 119 263.18257 -31.52587 95.33086 17.99310 8.0 3.00754 396.20281 59.75164 751.59404 846.92490 True 1.763e-10 2.947e-11
80 92 270.15899 -23.98049 192.41910 46.69483 8.0 5.38562 494.88697 152.68893 901.04315 1093.46225 True 4.576e-10 5.278e-11
69 93 270.40919 -23.47797 199.75682 46.45624 8.0 5.36583 507.14543 151.74287 844.50081 1044.25763 True 4.553e-10 5.259e-11
32 98 271.16056 -21.74479 229.82409 55.11421 7.0 5.91212 539.20902 179.26857 806.59952 1036.42361 True 5.401e-10 5.794e-11
52 60 272.43197 -23.54282 774.66618 61.05926 7.0 4.76383 318.62545 199.21166 317.75376 1092.41995 True 5.984e-10 4.669e-11
200 99 266.41449 -28.97054 1036.45364 144.33603 7.0 8.05908 1096.56231 476.57624 -899.15077 137.30287 True 1.414e-09 7.898e-11
Note that we used the instrument point-spread-function (PSF) as kernel, so the hypothesis we test is the presence of a point source. In order to test for extended sources we would have to use as kernel an extended template convolved by the PSF. Alternatively, we can compute the significance of an extended excess using the Li & Ma formalism, which is faster as no fitting is involve.
What next?#
In this notebook, we have seen how to work with images and compute TS and significance images from counts data, if a background estimate is already available.
Here’s some suggestions what to do next:
Look how background estimation is performed for IACTs with and without the high level interface in High level interface and Low level API notebooks, respectively
Learn about 2D model fitting in the 2D map fitting notebook
Find more about Fermi-LAT data analysis in the Fermi-LAT with Gammapy notebook
Use source candidates to build a model and perform a 3D fitting (see 3D detailed analysis, Multi instrument joint 3D and 1D analysis notebooks for some hints)
Total running time of the script: (0 minutes 12.589 seconds)
