Note
Go to the end to download the full example code or to run this example in your browser via Binder
1D spectrum simulation#
Simulate a number of spectral on-off observations of a source with a power-law spectral model using the CTA 1DC response and fit them with the assumed spectral model.
Prerequisites#
Knowledge of spectral extraction and datasets used in gammapy, see for instance the spectral analysis tutorial
Context#
To simulate a specific observation, it is not always necessary to simulate the full photon list. For many uses cases, simulating directly a reduced binned dataset is enough: the IRFs reduced in the correct geometry are combined with a source model to predict an actual number of counts per bin. The latter is then used to simulate a reduced dataset using Poisson probability distribution.
This can be done to check the feasibility of a measurement, to test whether fitted parameters really provide a good fit to the data etc.
Here we will see how to perform a 1D spectral simulation of a CTA observation, in particular, we will generate OFF observations following the template background stored in the CTA IRFs.
Objective: simulate a number of spectral ON-OFF observations of a source with a power-law spectral model with CTA using the CTA 1DC response, fit them with the assumed spectral model and check that the distribution of fitted parameters is consistent with the input values.
Proposed approach#
We will use the following classes and functions:
import numpy as np
import astropy.units as u
from astropy.coordinates import Angle, SkyCoord
from regions import CircleSkyRegion
# %matplotlib inline
import matplotlib.pyplot as plt
Setup#
from IPython.display import display
from gammapy.data import Observation, observatory_locations
from gammapy.datasets import Datasets, SpectrumDataset, SpectrumDatasetOnOff
from gammapy.irf import load_irf_dict_from_file
from gammapy.makers import SpectrumDatasetMaker
from gammapy.maps import MapAxis, RegionGeom
from gammapy.modeling import Fit
from gammapy.modeling.models import PowerLawSpectralModel, SkyModel
Check setup#
from gammapy.utils.check import check_tutorials_setup
check_tutorials_setup()
System:
python_executable : /Users/mregeard/Workspace/dev/code/gammapy/gammapy/.tox/build_docs/bin/python
python_version : 3.9.16
machine : x86_64
system : Darwin
Gammapy package:
version : 1.1.dev1875+g29bbf0baf.d20231019
path : /Users/mregeard/Workspace/dev/code/gammapy/gammapy/.tox/build_docs/lib/python3.9/site-packages/gammapy
Other packages:
numpy : 1.26.0
scipy : 1.11.3
astropy : 5.2.2
regions : 0.7
click : 8.1.7
yaml : 6.0.1
IPython : 8.15.0
jupyterlab : not installed
matplotlib : 3.8.0
pandas : not installed
healpy : 1.16.5
iminuit : 2.24.0
sherpa : 4.15.1
naima : 0.10.0
emcee : 3.1.4
corner : 2.2.2
ray : 2.7.0
Gammapy environment variables:
GAMMAPY_DATA : /Users/mregeard/Workspace/data/gammapy-data/gammapy-datasets/dev
Simulation of a single spectrum#
To do a simulation, we need to define the observational parameters like
the livetime, the offset, the assumed integration radius, the energy
range to perform the simulation for and the choice of spectral model. We
then use an in-memory observation which is convolved with the IRFs to
get the predicted number of counts. This is Poisson fluctuated using
the fake() to get the simulated counts for each observation.
# Define simulation parameters parameters
livetime = 1 * u.h
pointing = SkyCoord(0, 0, unit="deg", frame="galactic")
offset = 0.5 * u.deg
# Reconstructed and true energy axis
energy_axis = MapAxis.from_edges(
np.logspace(-0.5, 1.0, 10), unit="TeV", name="energy", interp="log"
)
energy_axis_true = MapAxis.from_edges(
np.logspace(-1.2, 2.0, 31), unit="TeV", name="energy_true", interp="log"
)
on_region_radius = Angle("0.11 deg")
center = pointing.directional_offset_by(position_angle=0 * u.deg, separation=offset)
on_region = CircleSkyRegion(center=center, radius=on_region_radius)
# Define spectral model - a simple Power Law in this case
model_simu = PowerLawSpectralModel(
index=3.0,
amplitude=2.5e-12 * u.Unit("cm-2 s-1 TeV-1"),
reference=1 * u.TeV,
)
print(model_simu)
# we set the sky model used in the dataset
model = SkyModel(spectral_model=model_simu, name="source")
PowerLawSpectralModel
type name value unit error min max frozen is_norm link
-------- --------- ---------- -------------- --------- --- --- ------ ------- ----
spectral index 3.0000e+00 0.000e+00 nan nan False False
spectral amplitude 2.5000e-12 cm-2 s-1 TeV-1 0.000e+00 nan nan False True
spectral reference 1.0000e+00 TeV 0.000e+00 nan nan True False
Load the IRFs In this simulation, we use the CTA-1DC IRFs shipped with Gammapy.
irfs = load_irf_dict_from_file(
"$GAMMAPY_DATA/cta-1dc/caldb/data/cta/1dc/bcf/South_z20_50h/irf_file.fits"
)
location = observatory_locations["cta_south"]
obs = Observation.create(
pointing=pointing,
livetime=livetime,
irfs=irfs,
location=location,
)
print(obs)
/Users/mregeard/Workspace/dev/code/gammapy/gammapy/.tox/build_docs/lib/python3.9/site-packages/astropy/units/core.py:2097: UnitsWarning: '1/s/MeV/sr' did not parse as fits unit: Numeric factor not supported by FITS If this is meant to be a custom unit, define it with 'u.def_unit'. To have it recognized inside a file reader or other code, enable it with 'u.add_enabled_units'. For details, see https://docs.astropy.org/en/latest/units/combining_and_defining.html
warnings.warn(msg, UnitsWarning)
Invalid unit found in background table! Assuming (s-1 MeV-1 sr-1)
/Users/mregeard/Workspace/dev/code/gammapy/gammapy/.tox/build_docs/lib/python3.9/site-packages/gammapy/data/observations.py:260: GammapyDeprecationWarning: Pointing will be required to be provided as FixedPointingInfo
warnings.warn(
Observation
obs id : 0
tstart : 51544.00
tstop : 51544.04
duration : 3600.00 s
pointing (icrs) : 266.4 deg, -28.9 deg
deadtime fraction : 0.0%
Simulate a spectra
# Make the SpectrumDataset
geom = RegionGeom.create(region=on_region, axes=[energy_axis])
dataset_empty = SpectrumDataset.create(
geom=geom, energy_axis_true=energy_axis_true, name="obs-0"
)
maker = SpectrumDatasetMaker(selection=["exposure", "edisp", "background"])
dataset = maker.run(dataset_empty, obs)
# Set the model on the dataset, and fake
dataset.models = model
dataset.fake(random_state=42)
print(dataset)
SpectrumDataset
---------------
Name : obs-0
Total counts : 298
Total background counts : 22.29
Total excess counts : 275.71
Predicted counts : 303.66
Predicted background counts : 22.29
Predicted excess counts : 281.37
Exposure min : 2.53e+08 m2 s
Exposure max : 1.77e+10 m2 s
Number of total bins : 9
Number of fit bins : 9
Fit statistic type : cash
Fit statistic value (-2 log(L)) : -1811.58
Number of models : 1
Number of parameters : 3
Number of free parameters : 2
Component 0: SkyModel
Name : source
Datasets names : None
Spectral model type : PowerLawSpectralModel
Spatial model type :
Temporal model type :
Parameters:
index : 3.000 +/- 0.00
amplitude : 2.50e-12 +/- 0.0e+00 1 / (cm2 s TeV)
reference (frozen): 1.000 TeV
You can see that background counts are now simulated
On-Off analysis#
To do an on off spectral analysis, which is the usual science case, the
standard would be to use SpectrumDatasetOnOff, which uses the
acceptance to fake off-counts. Please also refer to the Dataset simulations
section in the Spectral analysis with energy-dependent directional cuts tutorial,
dealing with simulations based on observations of real off counts.
dataset_on_off = SpectrumDatasetOnOff.from_spectrum_dataset(
dataset=dataset, acceptance=1, acceptance_off=5
)
dataset_on_off.fake(npred_background=dataset.npred_background())
print(dataset_on_off)
SpectrumDatasetOnOff
--------------------
Name : vrhn_cd4
Total counts : 292
Total background counts : 20.20
Total excess counts : 271.80
Predicted counts : 301.43
Predicted background counts : 20.06
Predicted excess counts : 281.37
Exposure min : 2.53e+08 m2 s
Exposure max : 1.77e+10 m2 s
Number of total bins : 9
Number of fit bins : 9
Fit statistic type : wstat
Fit statistic value (-2 log(L)) : 8.62
Number of models : 1
Number of parameters : 3
Number of free parameters : 2
Component 0: SkyModel
Name : source
Datasets names : None
Spectral model type : PowerLawSpectralModel
Spatial model type :
Temporal model type :
Parameters:
index : 3.000 +/- 0.00
amplitude : 2.50e-12 +/- 0.0e+00 1 / (cm2 s TeV)
reference (frozen): 1.000 TeV
Total counts_off : 101
Acceptance : 9
Acceptance off : 45
You can see that off counts are now simulated as well. We now simulate several spectra using the same set of observation conditions.
n_obs = 100
datasets = Datasets()
for idx in range(n_obs):
dataset_on_off.fake(random_state=idx, npred_background=dataset.npred_background())
dataset_fake = dataset_on_off.copy(name=f"obs-{idx}")
dataset_fake.meta_table["OBS_ID"] = [idx]
datasets.append(dataset_fake)
table = datasets.info_table()
display(table)
name counts excess sqrt_ts ... counts_off acceptance acceptance_off alpha
...
------ ------ ----------------- ------------------ ... ---------- ---------- ----------------- -------------------
obs-0 317 298.6000061035156 27.08240180813126 ... 92 9.0 45.0 0.20000000298023224
obs-1 275 253.0 23.76785365487285 ... 110 9.0 45.0 0.2
obs-2 293 272.4 25.17110555404655 ... 103 9.0 45.0 0.2
obs-3 280 257.6 23.982951737405354 ... 112 9.0 45.00000000000001 0.19999999999999998
obs-4 337 316.4 27.682709945184747 ... 103 9.0 45.0 0.2
obs-5 283 258.6 23.727154782347895 ... 122 9.0 45.0 0.2
obs-6 330 307.6 26.889184475727866 ... 112 9.0 44.99999999999999 0.20000000000000004
obs-7 283 257.2 23.43087974795853 ... 129 9.0 45.0 0.2
obs-8 308 284.6 25.42049273328331 ... 117 9.0 45.0 0.2
obs-9 299 278.6 25.57085071486863 ... 102 9.0 45.00000000000001 0.19999999999999998
obs-10 310 294.8 27.488972161356774 ... 76 9.0 45.00000000000001 0.19999999999999998
obs-11 285 261.0 23.933833745454685 ... 120 9.0 44.99999999999999 0.20000000000000004
obs-12 299 278.0 25.4325263895117 ... 105 9.0 44.99999999999999 0.20000000000000004
obs-13 309 287.4 25.877406235012618 ... 108 9.0 45.0 0.2
obs-14 320 297.4 26.28282602819255 ... 113 9.0 45.00000000000001 0.19999999999999998
obs-15 283 261.0 24.25408979304137 ... 110 9.0 45.0 0.2
obs-16 298 273.8 24.664218201697352 ... 121 9.0 45.0 0.2
obs-17 301 272.8 24.01180151925227 ... 141 9.0 45.0 0.2
obs-18 311 289.2 25.947476976949815 ... 109 9.0 45.0 0.2
obs-19 280 257.6 23.982951737405376 ... 112 9.0 45.0 0.2
obs-20 327 304.2 26.63324286828024 ... 114 9.0 44.99999999999999 0.20000000000000004
obs-21 286 266.8 25.08332073068164 ... 96 9.0 45.00000000000001 0.19999999999999998
... ... ... ... ... ... ... ... ...
obs-77 304 285.0 26.192157113580464 ... 95 9.0 45.0 0.2
obs-78 337 314.4 27.23331180179332 ... 113 9.0 45.0 0.2
obs-79 315 294.6 26.4957236283439 ... 102 9.0 45.00000000000001 0.19999999999999998
obs-80 304 282.8 25.67868740385823 ... 106 9.0 44.99999999999999 0.20000000000000004
obs-81 301 281.6 25.922347414834622 ... 97 9.0 45.0 0.2
obs-82 280 258.0 24.072587044084237 ... 110 9.0 44.99999999999999 0.20000000000000004
obs-83 303 280.8 25.394928282299105 ... 111 9.0 44.99999999999999 0.20000000000000004
obs-84 269 247.8 23.580247140026987 ... 106 9.0 44.99999999999999 0.20000000000000004
obs-85 297 274.6 24.998935845735573 ... 112 9.0 45.00000000000001 0.19999999999999998
obs-86 286 268.2 25.42340896951546 ... 89 9.0 44.99999999999999 0.20000000000000004
obs-87 333 313.2 27.646851451147217 ... 99 9.0 45.0 0.2
obs-88 315 296.8 27.0172059251097 ... 91 9.0 44.99999999999999 0.20000000000000004
obs-89 287 265.0 24.49456558680515 ... 110 9.0 44.99999999999999 0.20000000000000004
obs-90 286 267.0 25.131221887043438 ... 95 9.0 44.99999999999999 0.20000000000000004
obs-91 285 259.8 23.67754591931069 ... 126 9.0 45.0 0.2
obs-92 313 289.4 25.664935420194176 ... 118 9.0 45.0 0.2
obs-93 302 283.2 26.123867522605497 ... 94 9.0 45.0 0.2
obs-94 322 300.2 26.574029757473202 ... 109 9.0 45.0 0.2
obs-95 305 280.6 25.030731260493152 ... 122 9.0 44.99999999999999 0.20000000000000004
obs-96 301 277.4 24.969845969421428 ... 118 9.0 45.0 0.2
obs-97 290 271.2 25.417982194454826 ... 94 9.0 45.0 0.2
obs-98 301 280.6 25.687832964675007 ... 102 9.0 45.0 0.2
obs-99 323 302.2 26.85707842376871 ... 104 9.0 45.0 0.2
Length = 100 rows
Before moving on to the fit let’s have a look at the simulated observations.
/Users/mregeard/Workspace/dev/code/gammapy/gammapy/examples/tutorials/analysis-1d/spectrum_simulation.py:211: UserWarning: FigureCanvasAgg is non-interactive, and thus cannot be shown
plt.show()
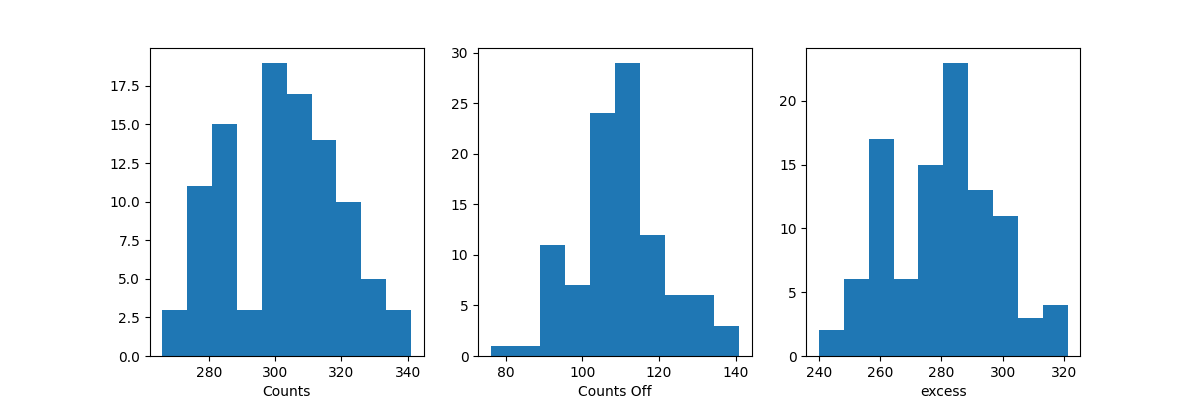
Now, we fit each simulated spectrum individually
results = []
fit = Fit()
for dataset in datasets:
dataset.models = model.copy()
result = fit.optimize(dataset)
results.append(
{
"index": result.parameters["index"].value,
"amplitude": result.parameters["amplitude"].value,
}
)
We take a look at the distribution of the fitted indices. This matches very well with the spectrum that we initially injected.
fig, ax = plt.subplots()
index = np.array([_["index"] for _ in results])
ax.hist(index, bins=10, alpha=0.5)
ax.axvline(x=model_simu.parameters["index"].value, color="red")
ax.set_xlabel("Reconstructed spectral index")
print(f"index: {index.mean()} += {index.std()}")
plt.show()
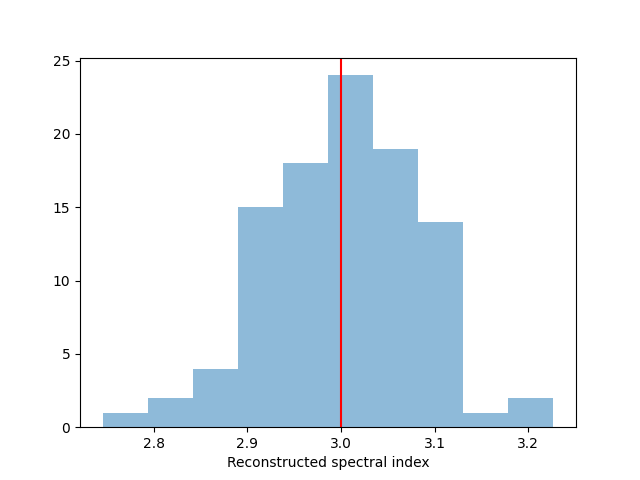
index: 3.0036925550377753 += 0.08081469527631224
/Users/mregeard/Workspace/dev/code/gammapy/gammapy/examples/tutorials/analysis-1d/spectrum_simulation.py:245: UserWarning: FigureCanvasAgg is non-interactive, and thus cannot be shown
plt.show()
Exercises#
Change the observation time to something longer or shorter. Does the observation and spectrum results change as you expected?
Change the spectral model, e.g. add a cutoff at 5 TeV, or put a steep-spectrum source with spectral index of 4.0
Simulate spectra with the spectral model we just defined. How much observation duration do you need to get back the injected parameters?
